利润问题作为国/省考行测科目中的“常驻嘉宾”,需要引起各位同学的重视。大家在能将公式熟练运用之后,想要快速拿分,就不能只一味地去设未知数求解,特别是遇到一些无具体数值的题目,我们要学会使用特值法,这样可让大家提高做题的速度。
我们一起来看下边的例题,解题时给出两种不同的方法,希望大家能从中体会到使用特值法的优势。
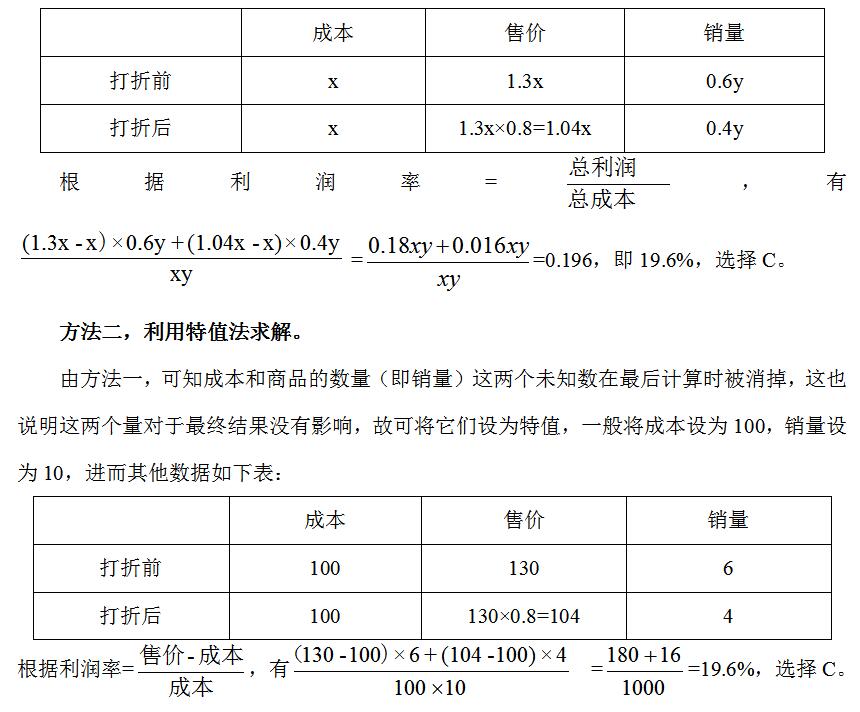
【例1】某商店新购进一批商品,按30%的利润定价,售出60%后,打八折后全部售出,问该商店出售这批商品最终获得的实际利润率是多少?
A.17.6%
B.18.6%
C.19.6%
D.20.6%
答案:C
【解析】方法一,利用常规的方程法求解。设单件商品的成本为x,这批商品共y件,根据题意梳理信息如下:
通过两种方法的对比,大家可以发现,方法二计算起来相对比较简单,基本上口算即可,这在考试时会让我们提高做题的速度。
【点拨】在利润问题中,当题干中给出一组或多组相对关系时,如例题给出的是利润率和销量的占比,并未给出具体带单位的数值时,我们可以考虑将成本、销量设为特值,一般成本设为100,销量设为10或100,进而可利用特值法快速解题。
通过例题的学习,接下来请大家尝试用特值法求解下题。
【例2】一批办公用品,经销商按期望获得100%的利润来定价,结果只销售掉70%。为了尽早销售掉剩下的办公用品,经销商决定打折出售,为了获得的全部利润是原来期望利润的91%,则经销商所打的折扣为:
A.六折
B.七折
C.八五折
D.九折
答案:C
【解析】本题未给带单位的具体数值,给的是相对量,可考虑用特值法求解。设单件成本为100,总量为10,设剩余办公用品打n折销售,结合题意其他数据如下:
根据全部利润是原来期望利润的91%列方程,折前利润为(200-100)×7,折后利润为(20n-100)×3,期望利润为(200-100)×10,则有(200-100)×7+(20n-100)×3=(200-100)×10×91%,整理得700+60n-300=910,60n=510,n=8.5,即八五折,选择C。