牛吃草问题是公考数量中一种非常典型的问题。由于其特征明显、公式简单,因此这一题型是考生拿分的重要题型。但也由于其过于简单,近年来公考中牛吃草问题不再是常客。实际上在整个公考数量中,牛吃草问题仍占有一席之地,只不过考查的方式变得多种多样,更侧重于对公式的理解,而非使用。
牛吃草的本质是行程问题中的追及问题,可以想象成草以一定的速度在生长,牛以更快的速度在吃草,牛吃草总量=原有草量+新增草量。其中,牛吃草的总量等于牛吃草的速度乘以牛吃草的时间;新增草量等于草的生长速度乘以草的生长时间。因此套用行程问题中的追及公式,也就得到了牛吃草问题的核心解法:y=(N-x)×T。
这个公式中,y代表原有草量、N代表牛的头数、x代表草的增速、T代表时间。隐含的假设为每头牛每天的吃草量为1(即牛吃草速度)。
牛吃草典型的考法有抽水机抽水、检票口检票、资源开采等。而牛吃草的特征也非常的明显,题干中出现排比句,类似于N1数量……需要T1时间;N2数量……需要T2时间……就可以判断为牛吃草问题。
先来看几道简单的牛吃草问题。
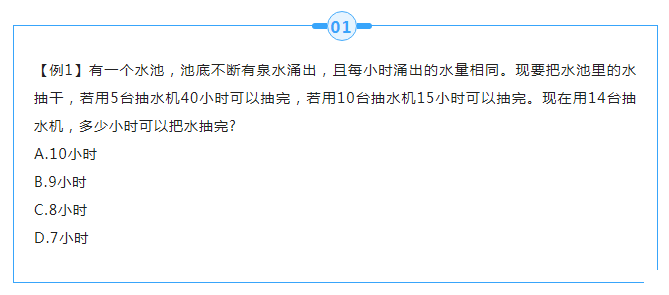
【答案】A
【解析】第一步,本题考查牛吃草问题,用方程法解题。
第二步,设水池里的水量为y,每小时涌出的水量为x,根据40小时抽完可得y=(5-x)×40,根据15小时抽完可得y=(10-x)×15,解得x=2,y=120。
第三步,设使用14台抽水机抽完水需要时间为t小时,则120=(14-2)×t,解得t=10。
因此,选择A选项。
此题中,“若用……若用”的排比句结构非常明显,直接代入公式解方程即可得到答案。然而这种考查方式已经很少见到,目前考查的牛吃草问题,往往需要首先判断哪一个量是草,哪一个量又是牛。一般来说,以恒定的速度一直在增加或消耗,就是草,它的速度即是x。
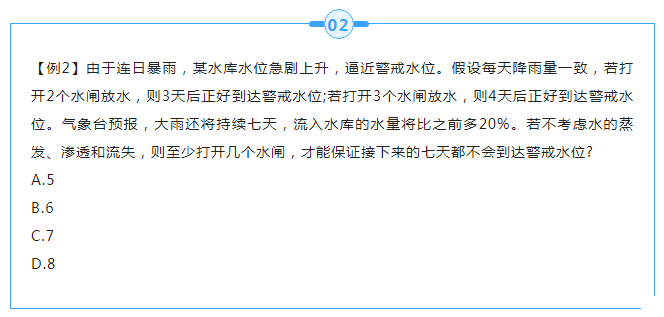
【答案】B
【解析】第一步,本题考查牛吃草问题。
第二步,假设原水位与警戒水位之间相差的蓄水量为y,每天流入水库的水量为x,由正好到达警戒水位得y=(x-2)×3,y=(x-3)×4,解得x=6,y=12。
第三步,由比之前多20%,可知现在每天流入水库的水量为6×(1+20%)=7.2。设至少打开N个水闸,可得12=(7.2-N)×7,解得N≈5.5,故至少打开6个水闸。
因此,选择B选项。
这道牛吃草问题不但需要根据“每天降雨量一致”来判断降雨量是草,还有一个典型的特征就是草的速度后期发生了变化,这也是近几年牛吃草问题的新特征——“草”的速度可能会变化、“牛”的头数也可能会变化;或者牛没有吃完,即草存量发生变化。但只要考生理解公式的核心概念,抓住公式的本质进行求解,牛吃草问题仍然是我们拿分的一种简单题型。
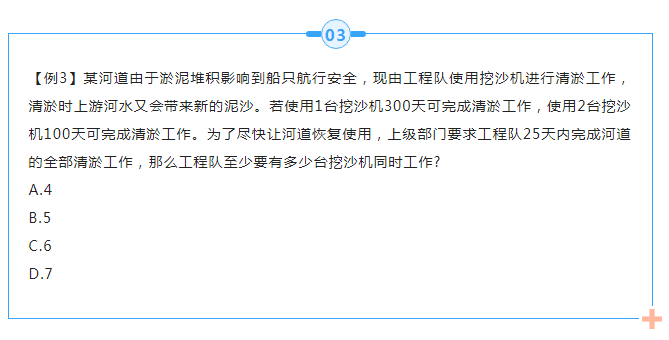
【答案】D
【解析】第一步,本题考查牛吃草问题。
第二步,设河道原来的淤泥堆积量为y,每天上游河水带来新的淤泥量为x,根据牛吃草问题公式:y=(N-x)×T,可列方程组:y=(1-x)×300,y=(2-x)×100。解得x=0.5,y=150。
第三步,设要想25天内完成清淤工作至少需要n台挖沙机,可列方程:150=(n-0.5)×25,解得n=6.5,即至少需要7台挖沙机。
因此,选择D选项。
通过这几道题目考生可以发现,牛吃草问题万变不离其宗,本质是:
①掌握牛吃草问题的核心概念
②灵活使用公式进行求解
③如果遇见分数小数要知道求整的方向。
如果能做到这3点,牛吃草问题必将成为考生拿分的囊中之题。